滤波
比如最简单的高斯模板，就是把模板内像素乘以不同的权值然后加起来作为模板的中心像素值，如果模板取值全为1，就是滑动平均；如果模板取值为高斯，就是加权滑动平均，权重是中间高，四周低，在频率上理解就是低通滤波器；如果模板取值为一些边缘检测的模板，结果就是模板左边的像素减右边的像素，或者右边的减左边的，得到的就是图像梯度，方向不同代表不同方向的边缘；
时域 $f(x)$ |
频域$F(u)$ |
|---|---|
| 连续+非周期 | 非周期+连续 |
| 连续+周期 | 非周期+离散 |
| 离散+非周期 | 周期+连续 |
| 离散+周期 | 周期+离散 |
而图像是一个二维的非周期离散的函数$f(x, y)$，对应在频域上是一个具有连续周期性的函数。而时域上的卷积对应频域上的乘积， 因此一张图片$x$和一个卷积核$w$进行卷积操作$(x * w)(t)$，相当于先把$x$和$w$进行傅里叶变换/z变换变换到频域之中得到$X$和$W$，然后再求$X \cdot W$。
图像中，像素值变化剧烈的部分对应这频域里的高频分量，变化和缓的部分对应着频域里的低频分量，因此如果一个卷积核具有低通滤波的特征的话，那一张图像与其进行卷积操作就可以得到保留图像中变化和缓的部分，即纹理等；如果一个卷积核具有高通滤波的特征的话，那一张图像与其进行卷积操作就可以得到保留图像中变化剧烈的部分，即边缘等。一张图像与若干不同的卷积核进行卷积操作，就可以得到它不同的频段上的特征。
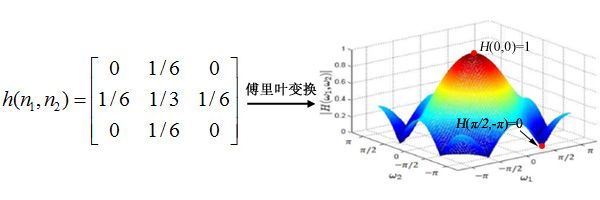↑表示一个低通的卷积核[https://blog.csdn.net/iracer/article/details/49330533]
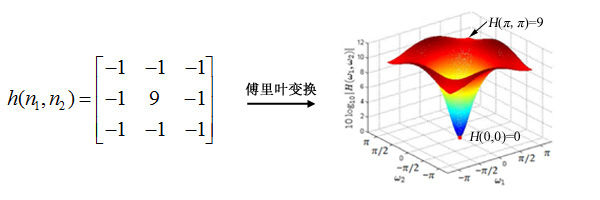↑表示一个高通的卷积核[https://blog.csdn.net/iracer/article/details/49330533]
投影
因为图像和卷积核的相乘累加操作就是图像局部patch和卷积核的内积操作，如果把patch和卷积核拉直，拉直的向量看成是向量空间中的向量，那么这个过程就是patch向卷积核方向上的投影，一幅图像和一个卷积核卷积，得到的结果就是图像各个patch在这个方向上的response map或者feature map；如果这样的卷积核有一组，我们可以把这一组看成一组基，得到的一组feature map就是原图像在这组基上的投影。常见的如用一组Garbor滤波器提取图像的特征，以及卷积神经网络中的第一层，图像在各个卷积核上的投影。
从这个角度上来讲，因为当patch和卷积核的方向越相近（余弦相似度）越高，那么该patch和卷积核的内积就越大，也就是说，卷积核选择图像中与其最相似的patch，得到的response越高，不同的卷积核选择不同的形状。