图神经网络及其在交通预测方面的应用

exiaohu 于 2019-11-24 发布

图神经网络

图神经网络可以粗略地分为基于谱的图神经网络和基于空间的图神经网络。其中前者从图的傅立叶变换而来，具有坚实的理论基础，在通过多番简化之后，其计算开销、局部性等已经能够满足大部分情形下的要求，但是它只能用来处理边上权重维数为$1$的无向图。而后者虽然缺乏理论基础，但是可以用来处理更加广泛的图结构数据，如有向图、多权图等。

基于谱的图神经网络

图的傅立叶变换和拉普拉斯矩阵

首先，连续函数的傅立叶变换可以表示为：

\[\hat{f}(\omega) = \mathcal{F}[f(t)]=\int_{-\infty}^{\infty}f(t)e^{-i \omega t}dt. \tag{1.1}\]

其中$e^{-i \omega t}$是拉普拉斯算子$\nabla^2$的特征方程，即$\nabla^2 e^{-i \omega t} = \lambda e^{-i \omega t}$，通过它，函数$f(t)$就被映射到了以${e^{-i \omega t}}$为基向量的空间中。与此类似，图的傅立叶变换定义为将其映射到以图的拉普拉斯矩阵的特征矩阵为基向量的空间中。

而图的拉普拉斯矩阵是什么呢？连续函数的拉普拉斯算子$\nabla^2 = \nabla \cdot \nabla$的第二个$\nabla$代表梯度，第一个$\nabla$代表散度，即连续的拉普拉斯算子指的是其梯度的散度。与此类似，图的拉普拉斯矩阵是图上的信号的梯度的散度。那么问题就变成了如何定义图上的梯度和散度。

我们知道，梯度是一个向量，其中的每一个分量都代表函数值在定义域的一个正交方向上下降的速度。在图中，每一个结点$i$都可以通过一个函数$f(\cdot)$映射到实域中的一个实数值$f(i) \in \mathbb{R}$，这样每一个结点都关联着一个实数值，这样假设图中有$N$个结点，$f(\cdot )$可以简写为一个向量$f \in \mathbb{R}^N$，这样的向量就称为图上的信号。

我们知道，函数的定义域可以分为若干个正交的方向，一个函数的定义域能够正交地分为几个方向是固定的，每个方向上都有一个梯度的分量，而梯度在这个方向上的分量$\nabla f_i = \frac{\partial f}{\partial x_i} = \frac{f(x + \triangle x) - f(x)}{\triangle x_i}$，即在这个方向上函数值的差值与距离的比值。而图上的每一个结点都连接有数目不等的边，这些边都可以看作是互相正交的方向，这样，与此类似，图上的信号在某一个方向（某一条边）上的梯度分量就是在这条边上图信号的差值与距离的比值。

那么问题就变成了如何定义图上两个结点在某一条边上的距离。我们知道，图上边上的权重代表这两个结点的接近程度（越近越大），而距离的定义与此相反，其表示两个结点离得有多远（越远越大），这样，距离可以定义为边上权重的倒数，这样，图上的两个结点$i$和$j$在边$e_{ij}$上的梯度就可以定义为$\nabla f_{ij}=(f_i - f_j) A_{ij}$，其中$A_{ij}$是边$e_{ij}$上的权重。

如百度百科所说，”散度是描述空气从周围汇合到某一处或从某一处流散开来程度的量“。函数的散度即其梯度在各个方向上的分量的和，$\nabla^2f=\sum_i{\nabla_i{f}}$。与此类似，图在结点$i$上的散度定义为该图信号在与该结点相连的每一条边上的梯度之和，即

\[\nabla^2 f_i = \sum_j{(f_i - f_j)A_{ij}} = \left[ \begin{matrix} f_i - f_1 & f_i - f_2 & \ldots & f_i - f_N \end{matrix} \right] \left[ \begin{matrix} A_{i,1} \\ A_{i,2} \\ \vdots \\ A_{i,N} \end{matrix} \right] = (f_i^T - f^T) \cdot A_i = f_i A_i - A_i^T \cdot f, \tag{1.2}\]

其中$\cdot$是向量的点积。将$f_i A_i$简记为$f_i d_i$，其中$d_i=\sum_{j=1}^N{A_{ij}}$为结点$i$的度，即与其相连的所有边上的权重之和，上式可以简写为$\nabla^2 f_i = f_i d_i - A_i^T \cdot f$，因此，图在每个结点上的散度即

\[\nabla^2 f = \left[ \begin{matrix} f_1 d_1 - f^T \cdot A_1 \\ f_2 d_2 - f^T \cdot A_2 \\ \vdots \\ f_N d_N - f^T \cdot A_N \end{matrix} \right] = \left[ \begin{matrix} d_1 & 0 & \ldots & 0 \\ 0 & d_2 & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & d_N \end{matrix} \right] \left[ \begin{matrix} f_1 \\ f_2 \\ \vdots \\ f_N \end{matrix} \right] - \left[ \begin{matrix} A_1^T \\ A_2^T \\ \vdots \\ A_N^T \end{matrix} \right] \left[ \begin{matrix} f_1 \\ f_2 \\ \vdots \\ f_N \end{matrix} \right] = (D - A)f,\tag{1.3}\]

其中，$D$是对角线元素为图中每个结点的度的对角矩阵，$A$是该图的邻接矩阵，$A_{ij}$是结点$i$到结点$j$的权重。这样，图的散度$\nabla^2 f=(D-A)f$，即图的拉普拉斯矩阵$L$就是$\nabla^2=D-A$ 。

如前文所述，图的傅立叶变换定义为其与图的拉普拉斯矩阵的特征矩阵的卷积。那么，图的拉普拉斯矩阵经过特征分解$L=D-A=U \Lambda U^T$之后，在结点$i$上的图的傅立叶变换就是$\hat{f}i=\sum{j=1}^N{f_j U_j^T}$，那么在所有结点上同时做傅立叶变换，即

\[\hat{f} = \mathcal{F}[f] = U^T f.\tag{1.4}\]

傅立叶逆变换就是$f=U\hat{f}$。

最后，众所周知的是，在频域上的卷积可以转换为在谱域中的点积，然后转换回频域来进行运算。那么，图的卷积可以表示为

\[f \star_{\mathcal{G}} g = \mathcal{F}^{-1}[\mathcal{F}[f] \cdot \mathcal{F}[g]] = U((U^T f) \cdot (U^T g)) = U ((U^T g) \cdot (U^T f) ),\tag{1.5}\]

其中，$\star_{\mathcal{G}}$表示图卷积；$\cdot$表示向量点积，满足交换率；$g$是卷积核，可以通过学习得到。将$U^T g$看作可以学习的卷积核$g_{\theta}$，图卷积就是

\[f \star_{\mathcal{G}} g_{\theta} = U(g_{\theta} \cdot (U^T f))=Ug_\theta U^T f. \tag{1.6}\]

其中

\[g_{\theta}= \left[ \begin{matrix} \theta_1 & \ldots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \ldots & \theta_N \\ \end{matrix} \right].\tag{1.7}\]

接下来要介绍的图上频域卷积的工作，都是在此基础上做文章。

Deep Convolutional Networks on Graph-Structured Data The emerging field of signal processing on graphs: Extending high-dimensional data analysis to networks and other irregular domains

切比雪夫多项式展开

如上所述，图卷积可以写成$f \star_{\mathcal{G}} g_{\theta} = Ug_\theta U^T f$，其中$g_\theta$是一个可训练的对角矩阵，直接计算该式需要涉及到对图的拉普拉斯矩阵的特征分解和两组矩阵乘法，时间复杂度过大。而$g_\theta$可以看成是一个参数化的变换$g_\theta(\Lambda)$，其通过参数化的线性变换将$\Lambda$变换为$g_\theta$。此时，图卷积可以写作：

\[f \star_{\mathcal{G}} g_{\theta} = Ug_\theta (\Lambda) U^T f = g_\theta (U \Lambda U^T) f = g_\theta (L) f.\tag{1.8}\]

使用切比雪夫多项式对$g_\theta (L)$进行展开，截取前$K$项，上式可以写作：

\[f \star_{\mathcal{G}} g_{\theta}= g_\theta (L) f = \sum_{k=0}^{K-1}{\theta_k T_k (L)} f,\tag{1.9}\]

其中$T_k(\cdot)$是切比雪夫多项式的第$k$项，$T_0(A)=I$，$T_1(A)=A$和$T_k(A)=2AT_{k-1}(A)-T_{k-2}(A)$，而$\theta \in \mathbb{R}^K$是可训练参数。图卷积的$K$阶的切比雪夫多项式展开形式可以看作是考虑每一个结点的$K$跳邻居，即图卷积每一层的感受野大小是$K$。

Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering

归一化的(normalized)和放缩的(scaled)拉普拉斯矩阵

因为原始的拉普拉斯矩阵会扩大输入信号的范围，使输入信号的分布偏移，因此对拉普拉斯矩阵进行归一化和放缩。拉普拉斯矩阵的归一化方法有几种，最常见的方法就是：

\[L = D^{-1/2} (L-A) D^{-1/2} = I-D^{-1/2}AD^{-1/2}.\tag{1.10}\]

若无说明，下文所提及的拉普拉斯矩阵$L$均为归一化后的拉普拉斯矩阵。而放缩的拉普拉斯矩阵：

\[\tilde{L} = \frac{2}{\lambda_{max}}L - I,\tag{1.11}\]

其中，$\lambda_{max}$是拉普拉斯矩阵$L$的最大的特征值，有时候会使用$2$来对其近似。

一阶切比雪夫多项式展开和GCN

然而由于切比雪夫的$K$阶展开仍旧需要较大的计算量，所以进一步对其进行简化，只取其$1$阶展开，图卷积的公式可以进一步简化为：

\[f \star_{\mathcal{G}} g_{\theta}= (\theta_0 + \theta_1 L) f.\tag{1.12}\]

对其进一步简化，即取$\theta_0=-\theta_1=\theta$，可训练参数的数目最终降低为$1$，这样就得到GCN(Graph Convolutional Network)：

\[f \star_{\mathcal{G}} g_{\theta}= (\theta - \theta L) f = \theta (I - D^{-1/2}(D-A)D^{-1/2}) f = \theta D^{-1/2}AD^{-1/2}f,\tag{1.13}\]

其中$\theta\in \mathbb{R}$是可训练参数。这是在图上的信号是$1$维的情况，而在图卷积操作的输入和输出特征都是多维的情形下，假设输入信号$f\in\mathbb{R}^{N \times d}$，输出信号$f’\in\mathbb{R}^{N \times d’}$，图卷积可以写作：

\[f'=f \star_{\mathcal{G}} g_{\theta} = D^{-1/2}AD^{-1/2}f\Theta,\tag{1.14}\]

其中，$\Theta\in\mathbb{R}^{d \times d’}$是可训练参数。

Semi-Supervised Classification with Graph Convolutional Networks

基于空间的图神经网络

基于谱的图神经网络尽管具有坚实的理论基础，然而其理论基础也限制了其在形形色色，变化万千的图结构数据上的应用。而基于空间的图神经网络是不基于谱的图神经网络的总称，它们产生的动机各不一样，但是都是为了寻找一种能够良好地局部、并行、泛化、快速对图的拓扑信息和图信号进行提取的方法。

图卷积神经网络 PATCHY-SAN

将卷积神经网络(CNN)扩展到任意的图结构面临两个挑战：

首先，以二维图像为例，CNN将固定大小的卷积核应用到每一个固定大小的局部(3x3或5x5等)上，这是因为图像是很规整的网格型结构，在图像中，每一个像素周围都具有固定数目(8个)的相邻像素。而在任意的图结构上，每个结点及其连接关系都是任意的，因此与一个结点相邻的结点数目不固定，这就导致产生了第一个问题，即固定大小的卷积核难以在不同的结点上共享。这就要求局部的图卷积运算必须对运算数据的数目不敏感。

其次，就标准的图像卷积操作而言，不仅每个像素周围的相邻像素数目固定，其相邻像素的相对顺序也是固定的。即从一个相邻像素开始，可以逐次由内而外，按照顺时针方向，可以遍历一边所有的相邻像素，而每次遍历，每个相邻像素的访问顺序也是固定的。这样，可以按照标准的离散卷积操作，为每一个相邻像素和卷积核中的每一个元素编号，然后与对应编号相乘，加权求和。然而在任意的图结构中，与一个结点相邻的结点并没有一个确定的序列关系，即调换任意两个结点的编号并不改变图的结构。这就导致局部的图卷积运算必须对运算数据的顺序不敏感。

综上所述，在图卷积的过程中面临的两个主要问题是“数据规模无关(size-invariant)”和“排列无关(permutation-invariant)”。为了解决这两个问题，基于一个图的集合，PATCHY-SAN采用如下解决方法：

  1. 首先从图中选择固定长度的一个结点序列：具体的做法是，先根据某种准则选择为图中的每个结点产生一个排列，基本的思路是让附近结构相似的结点在排列中处于相近的位置，然后按照该排列和固定步长遍历图中的每个结点，选择遍历到的结点进行下一步，当遍历完所有结点后，若还没有达到预先设置的长度，就向选择出的结点后添加空结点；
  2. 然后，为每个选出的结点确定一个固定大小的感受野：具体的做法是，以每个选择出来的结点为起始结点，对该图进行广度优先搜索，一层一层由内而外将该结点的邻居结点加到该结点的邻居子图中，直到没有结点可以遍历或者选择的结点数大于或等于感受野的大小。注意，此时该结点的邻居子图中的结点数目与感受野的大小不一等相等；
  3. 对选择的邻居子图进行归一化：具体的做法是，首先通过某种准则对上面选出的邻居子图中的结点进行排序，基本的思路是让附近结构相似的结点在排列中处于相近的位置，然后从排序的结果中去掉尾部节点或者填充空结点得到每个选择结点的感受野；
  4. 在每个邻居子图上应用标准卷积操作。因为经过上面的操作，每个结点有了固定大小的感受野，每个感受野中都含有固定顺序的结点序列，这样就解决了上文提到的两个问题，从而可以应用现有的卷积操作来处理图结构的数据。

Learning Convolutional Neural Networks for Graphs

图注意力神经网络 GAT

上文所述的几种图神经网络操作要么需要矩阵的特征分解、求逆等运算量比较大的操作，要么需要在进行图卷积时知道图的结构，这样就不适于处理大规模的图结构数据。为了解决这样的问题，GAT(Graph Attention Network)通过Self-Attention机制来进行局部的图运算。

将该层图卷积结点$i$的输入特征记为$h_i\in \mathbb{R}^{d}$，该层图卷积结点$i$的输出特征记为$h’_i \in \mathbb{R}^{d’}$，首先通过一个共享的线性变换$W\in\mathbb{R}^{d’\times d}$将所有结点的特征进行变换，然后通过一个共享的注意力机制$a:\mathbb{R}^{d’}\times\mathbb{R}^{d’}\mapsto\mathbb{R}$计算注意力系数，这样的注意力机制可以是普通的注意力，也可以是多头的注意力机制(multi-head attention)，在GAT的初始实现中，$a(Wh_i, Wh_j)=\text{LeakyReLU}(w^T[Wh_i|Wh_j])$， $w \in \mathbb{R}^{2d’}$：

\[e_{ij}=a(Wh_i, Wh_j),\tag{1.15}\]

然后在结点$i$的所有邻居结点$j\in\mathcal{N}_i$的注意力系数上应用$\text{softmax}$来进行归一化，通过这样的方式，注意力机制能够隐式地捕获图的结构信息和特征信息：===

\[\alpha_{ij}=\text{softmax}_j(e_{ij})=\frac{\text{exp}(e_{ij})}{\sum_{k\in\mathcal{N}_i}\text{exp}(e_{ik})},\tag{1.16}\]

最后，应用归一化的注意力权重对每个邻居结点的特征进行加权求和，就得到了每个结点的新的隐特征：

\[h'_i=\sigma(\sum_{j\in\mathcal{N}_i}\alpha_{ij}Wh_j).\tag{1.17}\]

GRAPH ATTENTION NETWORKS

扩散卷积神经网络 DCNN

作为另一种可以广泛应用于各类图相关任务的图卷积神经网络，扩散卷积的运算与基于谱的图卷积网络类似，可以应用于各类有权的或无权的、有向的或无向的图结构数据上。首先对图的邻接矩阵$A\in\mathbb{R}^{N \times N}$进行度归一化，得到转移矩阵$P$。常用的归一化方法是$P=D^{-1}A$，其中$D$是对角线元素为图的入度的对角矩阵，实际上相当于对$A$中的每一行进行$L_1$归一化。

DCNN(Diffusion-Convolutional Neural Networks)模型中的扩散卷积核可以认为是考虑到每两个结点之间连接的所有路径，其中较短的路径比更长的路径更重要。在得到的转移矩阵$P$的基础上，计算其幂序列$P^*\in\mathbb{R}^{N \times H \times N}$，其中，$P_{:,i,:}$表示的是$P$的$i$次幂。然后，对于结点分类任务而言，有输入特征$X\in\mathbb{R}^{N\times F}$， 新的结点$Z\in\mathbb{R}^{N\times H\times F}$表示可以通过下式获得：

\[Z = f(W\odot (P^*X)).\tag{1.18}\]

其中，$W\in\mathbb{R}^{H\times F}$是共享在所有结点上的可训练参数。就图分类任务而言，可以通过在所有结点上应用平均池化来得到图的表示$Z\in\mathbb{R}^{H\times F}$。最后，分类结果通过在$Z$上应用一个全连接网络和$softmax$激活函数得到。

Diffusion-Convolutional Neural Networks

动态边权重的图神经网络 ECC

上述的所有图神经网络都隐含一个条件，即在它们的运算过程中，每个结点都关联一个特征向量（或称图信号），而每条边都是有向或无向的、有权或无权的，但每条边上关联的权重是一个标量。为了解决边上存在多维权重的情形，ECC(Edge-Conditioned Convolution)被提出了。

假设在第$l$层图卷积的输入图中有$n$个结点，$m$条边，每个结点关联一个$d_l$维向量，每条边关联一个$s$维向量，这样就有图信号$X^l\in\mathbb{R}^{n\times d_l}$和边权重$L\in\mathbb{R}^{m\times s}$，结点$i$的邻域$\mathcal{N}_i$包含$i$本身（图中包含自环）。在ECC中，第$l$层的图信号$X^l$是由第$l-1$层的图信号$X^{l-1}$加权求和得到的。

具体地，定义一个权重生成神经网络$F^l:\mathbb{R}^s\mapsto\mathbb{R}^{d_l\times d_{l-1}}$，它从边的权重向量生成一个面向特定边的卷积核$\Theta\in\mathbb{R}^{d_l\times d_{l-1}}$。这样，第$l$层的ECC卷积操作可以写成：

\[X^l_i=\frac{1}{|\mathcal{N}_i|}\sum_{j\in\mathcal{N}_i}{F^l(L(j,i);w^l)X^{l-1}_j} + b^l=\frac{1}{|\mathcal{N}_i|}\sum_{j\in\mathcal{N}_i}{\Theta_{j,i}^lX^{l-1}_j} + b^l.\tag{1.19}\]

Dynamic Edge-Conditioned Filters in Convolutional Neural Networks on Graphs

基于消息传递的图神经网络框架

图神经网络形形色色，变化万千，但大部分图神经网络都可以按照消息传递的框架来进行归纳与整理，这样对图神经网络的理解和实现，以及针对特定问题，设计新的图神经网络算法都有好处。

基于消息传递的框架，图神经网络的运算过程可以分为传递(pass)和读出(readout)。前者是指每个结点将自己的信息通过边传递给自己的邻居结点，而后者是指通过每个结点自身的信息和收到的邻居结点的信息对自身的状态进行更新。上面介绍的GCN、GAT和ECC等都可以用消息传递的框架表示。

Graph Neural Networks: A Review of Methods and Applications A Comprehensive Survey on Graph Neural Networks

其它神经网络技术

超图神经网络和动态超图神经网络

Hypergraph Neural Networks Dynamic Hypergraph Neural Networks

层次的图卷积和图池化

Hierarchical Graph Representation Learning with Differentiable Pooling An end-to-end deep learning architecture for graph classification Hierarchical Graph Convolutional Networks for Semi-supervised Node Classification Graph U-Nets Weighted Graph Cuts Without Eigenvectors: A Multilevel Approach. (Graclus算法)

图表示学习和网络嵌入

DeepWalk LINE Node2Vector SDNE DNGR Inductive Representation Learning on Large Graphs (GraphSAGE) HARP: Hierarchical Representation Learning for Networks

交通时空数据预测

这一两年来，基于图神经网络来进行交通预测层出不穷，已经成为主流方法。这些方法都使用图神经网络来对交通数据中的空间依赖进行建模，而根据其对时间依赖进行建模的方法不同，这些方法可以分为基于循环神经网络（主要是门限循环单元GRU）的方法与不基于循环神经网络（主要是一维卷积或因果卷积）的方法。根据这些方法解决的具体问题不同，它们又可以分为交通需求预测、OD矩阵预测和其它交通预测（交通流量、速度等）三类。

基于循环神经网络的方法

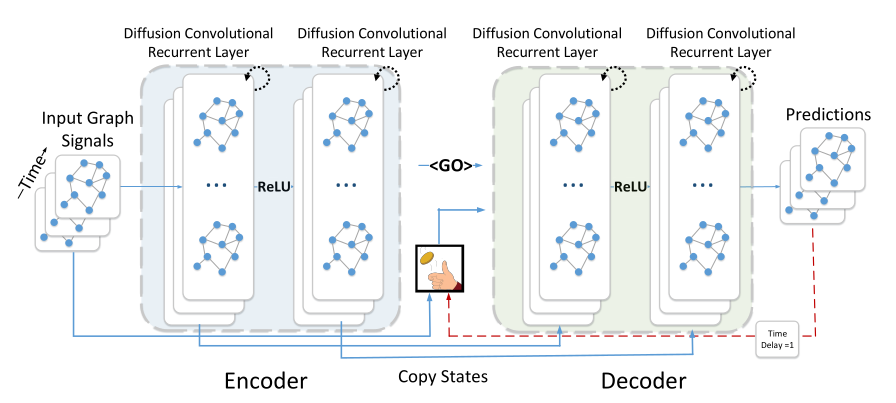
==DCRNN== (ICLR-2018)

DIFFUSION CONVOLUTIONAL RECURRENT NEURAL NETWORK: DATA-DRIVEN TRAFFIC FORECASTING

DCRNN结构图

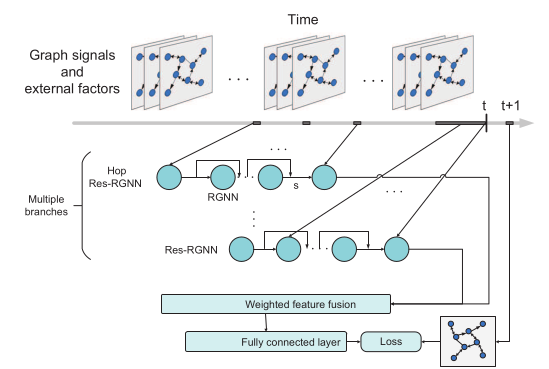
MRes-RGNN (AAAI-2019)

Gated Residual Recurrent Graph Neural Networks for Traffic Prediction

MRes-RGNN结构图

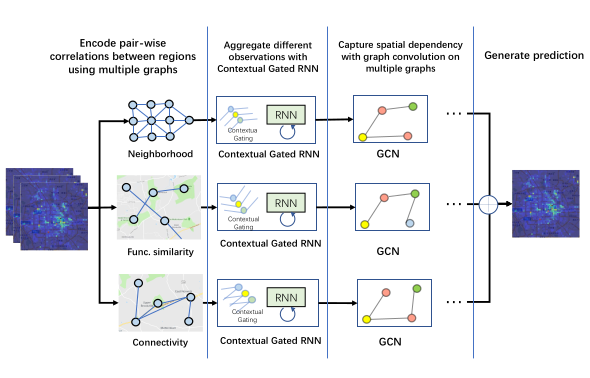
ST-MGCN (AAAI-2019)

Spatiotemporal Multi-Graph Convolution Network for Ride-hailing Demand Forecasting

ST-MGCN结构图

ODMP和GEML (KDD-2019)

Origin-Destination Matrix Prediction via Graph Convolution: a New Perspective of Passenger Demand Modeling

==ST-MetaNet== (KDD-2019)

Urban Traffic Prediction from Spatio-Temporal Data Using Deep Meta Learning

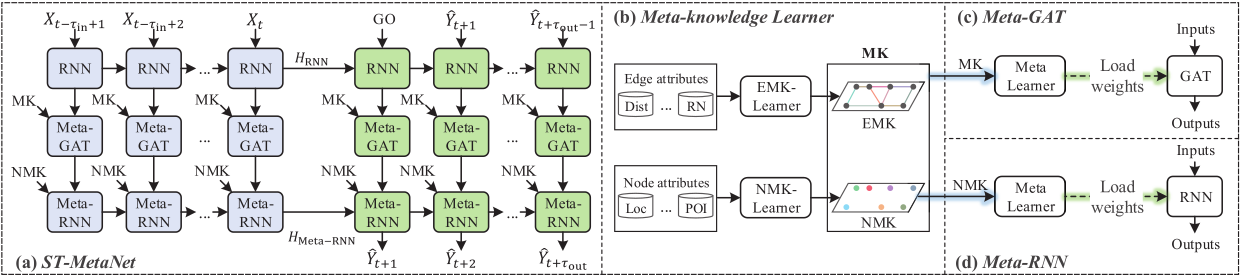
ST-MetaNet结构图

==MRA-BGCN== (AAAI-2020)

Multi-range attentive bicomponent graph convolutional network for traffic forecasting

==ST-UNet==

ST-UNet: A Spatio-Temporal U-Network for Graph-structured Time Series Modeling

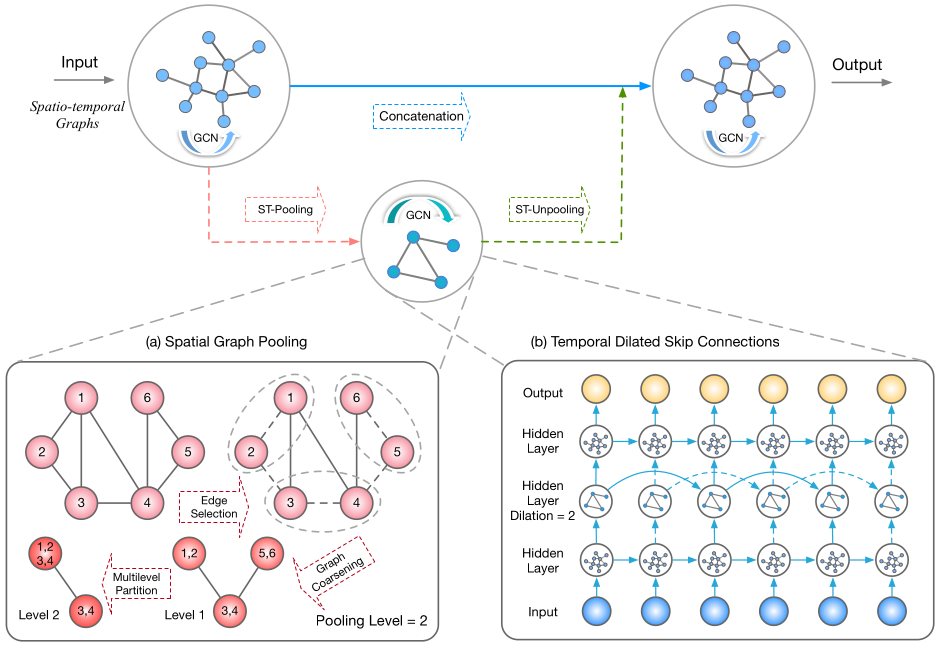
ST-UNet结构图

不基于循环神经网络的方法

STGCN (IJCAI-2018)

Spatio-Temporal Graph Convolutional Networks: A Deep Learning Framework for Traffic Forecasting

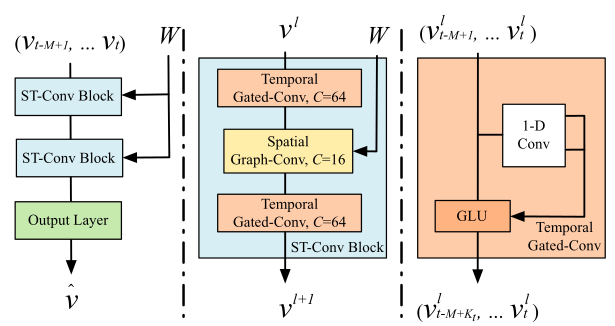
STGCN结构图

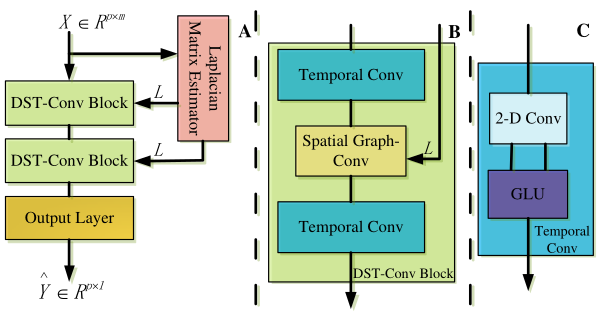
==DGCNN== (AAAI-2019)

Dynamic Spatial-Temporal Graph Convolutional Neural Networks for Traffic Forecasting

DGCNN结构图

ASTGCN (AAAI-2019)

Attention Based Spatial-Temporal Graph Convolutional Networks for Traffic Flow Forecasting

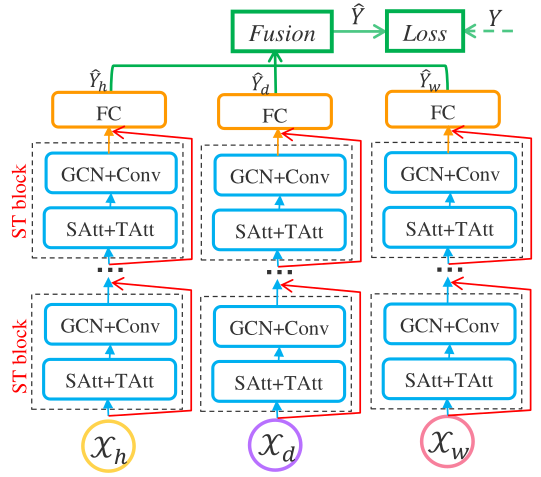
ASTGCN结构图

STG2Seq (IJCAI-2019)

STG2Seq: Spatial-temporal Graph to Sequence Model for Multi-step Passenger Demand Forecasting

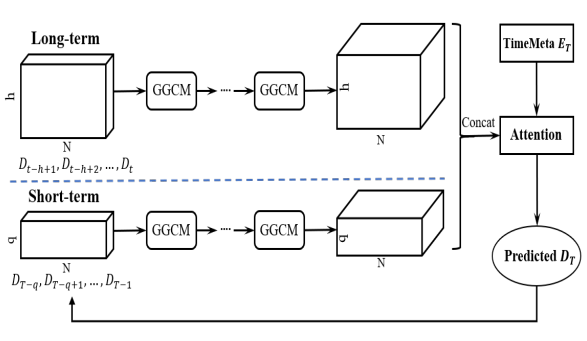
STG2Seq结构图

==Graph WaveNet== (IJCAI-2019)

Graph WaveNet for Deep Spatial-Temporal Graph Modeling

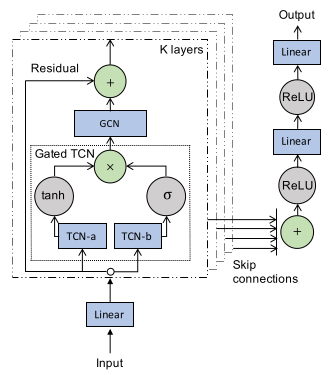
Graph WaveNet结构图

GSTNet (IJCAI-2019)

GSTNet: Global Spatial-Temporal Network for Traffic Flow Prediction

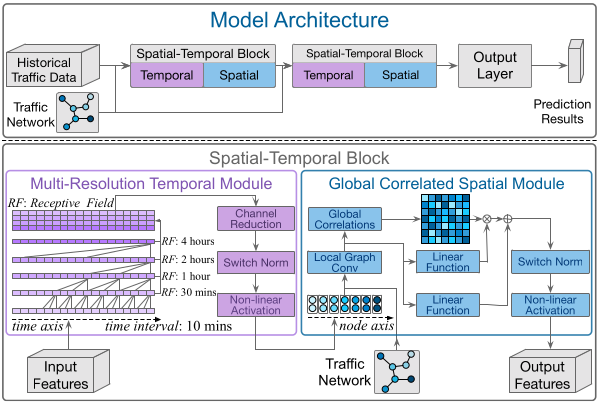
GSTNet结构图